Ejercicio 5 - Ecuación Cuadrática de la Forma Estándar

La forma estándar es:

y= a(x-h)^2 + k

Donde a, h y k, según sus valores la gráfica se moverá hacia arriba o hacia abajo, a la derecha o a la izquierda y también se podrá ensanchar o adelgazar.

a define si es ancha o delgada:

1- y= x^2

2- y= 3x^2

y= x^2

y= 3x^2

a= define si es ancha o delgada

h= define si se desplaza a la izquierda o a la derecha

k= define si va hacia arriba o hacia abajo

Ejercicio 6 - Conversión de Forma General a Forma Estándar

En ésta conversión utilizaremos el método para completar un trinomio cuadrado perfecto, en este caso será cuando el valor de a es igual a 1.

Encuentra el vértice y grafica la parábola:

y= x^2 - 6x + 13

Primero, identificamos los valores a, b y c:

a= 1

b= -6

c= 13

Segundo, aplicaremos la siguiente fórmula:

(b/2)^2

(-6/2)^2 = 9

Tercero, sumar y restar el resultado anterior:

y= x^2 - 6x + 9 - 9 + 13

Cuarto, los primeros 3 términos corresponden a un trinomio cuadrado perfecto que tenemos que factorizarlo para obtener un binomio al cuadrado:

y= x^2  -  6x  +  9   -9 +13

                                        Raíz  Signo  Raíz 

y= (x - 3)^2 + 4

Ahora podemos obtener el vértice con la siguiente fórmula, identificando los valores a, h y k:

y= (x - h)^2 + k 

a= 1

h= 3 

k= 4

V= (h,k)

V= (3,4)

Ahora que tenemos el primer punto o valor podemos tabular y con la información obtenida graficaremos: 

y= 2^2 - 6(2) + 13 = 5

y= 1^2 - 6(1) + 13 = 8

Características:

- Ramas arriba

- Concavidad positiva

- Vértice= (3,4)

- Eje de simetría= 3

- Mínimo= 4

Cuando el coeficiente cuadrático es diferente de 1:

Ejemplo: y= -4x^2 +24x +6

Primero se agrupan los términos cuadrático y lineal:

[-4x^+24x]+6

Segundo, se factoriza lo que agrupamos anteriormente tomando el término cuadrático:

-4[x^2-6x]+6

Tercero, se obtiene b del término lineal de todo lo que se encuentra adentro del corchete para aplicar (b/2)^2:

b=-6 (-6/2)^2 = -3^2= 9

Cuarto, se suma y se resta el valor obtenido dentro de los corchetes:

-4[x^2-6x+9-9]+6

Quinto, se factoriza para obtener el trinomio cuadrado perfecto (TCP) y se aplica jerarquía de operaciones:

-4(x-3)^2+36+6

-4(x-3)^2+42

y= (x-h)^2 +k

Ahora tenemos nuestra forma estándar, con la cuál empezamos a tabular y graficar:

a= -4

h= 3

k= 42

Vértice= (3,42)

-4(2)^2+24(2)+6=38

-4(1)^2+24(1)+6=26

Características:

-Ramas abajo

-Concavidad negativa

-Vértice (3,42)

-Eje de simetría 3

Máximo 42 

  

Ejercicio 4 - Análisis del Discriminante

El discriminante es la operación que se encuentra adentro del radical en la fórmula general. Si el discriminante es mayor a 0, obtendremos 2 raíces o soluciones  y el eje x es cortado en 2 puntos. Si es igual a 0, se obtendrá una raíz o solución y solamente se obtiene un punto sobre el eje x y ése será el vértice. Si es menor a 0, se tiene solución con 2 raíces complejas y conjugadas, las cuales no cortan al eje x. Para obtener la gráfica se tendrá que aplicar la formula del vértice o por medio del vértice y después tabular una unidad arriba y una unidad abajo.

Graficar la función:  F(x)= 2x^2 + x - 6

a= 2
b= 1
c= -6

Primero se tiene que obtener el punto x del vértice, con la siguiente fórmula:

X= -b/2a

x= -1/2(2)

x= -1/4 

x= -0.25

Ahora obtendremos la función de x ó y, sustituyendo los valores:

F(x)= 2(-.25)^2 - .25 - 6 = -6.125

Después se obtendrán un punto arriba y otro abajo por medio de la fórmula general: 

x1,x2=(-b±√(b^2-4ac))/2a

x1,x2=(-1±√(1^2-4(2)(-6)))/2(2)

x1,x2=(-1±√(1+48))/4

x1,x2=(-1±√(49))/4

x1,x2=-1±7/4

x1=-1+7/4 = 1.5

x2=-1-7/4 = -2

Y ahora podremos graficar con los puntos obtenidos, quedando de la siguiente forma:

Ejercicio 3 - Puntos Importantes de una Parábola

Graficar la siguiente función cuadrática a partir del vértice y las dos raíces, obtener también sus elementos.

F(x)= x^2 - 3x - 10

a= 1

b= -3

c= -10

Para obtener x se resuelve la siguiente fórmula:

x= -(b/2a)

x= -(-3/2)

x= 3/2

Ahora que obtuvimos el valor x, lo tomaremos como punto del vértice, y después sustituiremos x en la función cuadrática.

F(x)= (3/2)^2 - 3(3/2) - 10

F(x)= 9/4 - 9/2 - 10

F(x)= -(49/4)

Ahora tenemos nuestra vértice de la parábola:

Ahora que tenemos nuestro primer punto, emplearemos la función cuadrática en la fórmula general para obtener las x faltantes sacando la raíz.

x=(-b±√(b^2-4ac))/2a

x1,x2=(-(-3)±√((-3)^2-4(1)(-10)))/2(1)

x1,x2=(3±√(9 + 40))/2

x1,x2=(3±√(40))/2

x1,x2=3±7/2

x1=3+7/2 

x1= 5

x2=3-7/2

x2=-2

Y ahora que obtuvimos las x restantes, podremos llenar nuestra tabla, la cual queda de la siguiente forma:

Y por último elaboramos la representación gráfica de la función cuadrática (Parábola) con sus respectivos elementos.

La parábola tiene:

-Las ramas hacia arriba

-Concavidad positiva

-Vértice (3/2, -49/4)

-Eje de Simetría 3/2

-Punto mínimo -49/4

Ejercicio 2 - Elementos de la Parábola

Obtener elementos de la parábola y gráfica de la siguiente función cuadrática:

-x^2 + 2

Primero, se le tiene que dar valores a x, a continuación se muestra una tabulacion con valores proporcionados del -5 al 5:

A(x)=-(-5)^2 +2= -23

A(x)=-(-4)^2 +2= -14

A(x)=-(-3)^2 +2= -7

A(x)=-(-2)^2 +2= -2

A(x)=-(-1)^2 +2= 1

A(x)=-(0)^2  +2= 0

A(x)=-(2)^2 +2= -2

A(x)=-(3)^2 +2= -7

A(x)=-(4)^2 +2= -14

A(x)=-(5)^2 +2= -23

Ahora, con los datos obtenidos podemos realizar la parábola:

Ahora, analizaremos los elementos de la Parábola anterior:

-Tiene las ramas hacia abajo

-La concavidad es negativa

-Las coordenadas del vértice o su localización es (0,2)

-Eje de Simetría =  0

-Máximo = 2

Ejercicio 1 - Funciones Cuadráticas

Hay un terreno de forma rectangular, el cuál se quiere cercar con una malla de 120 metros. Sin embargo el terreno tiene barda por uno de sus lados, quedando de la siguiente forma: 

¿Qué área se puede cercar?

Primero, al considerar que es un rectángulo necesitamos las medidas de Perímetro y Área, los cuáles son:

              P= x+2b                   Área en función de x ó A(x)= xb

Ahora, debemos despejar b de la ecuación 1, por lo que queda de la siguiente forma:

b=120-x/2

b=60 / 1/2 

Y ahora b se sustituye en la ecuación 2, quedando de la siguiente manera:

A(x)= x(60 / 1/2) / 2

A(x)= 60x - 1/2x^2

En base a esta última sustituiremos x en un rango de 0-120, de la siguiente manera:

A(x)=60(0) - (0)^2= 0

A(x)=60(20) - (20)^2= 1000

A(x)=60(40) - (40)^2= 1600

A(x)=60(60) - (60)^2= 1800

A(x)=60(80) - (80)^2= 1600

A(x)=60(100) - (100)^2= 1000

A(x)=60(120) - (120)^2= 0 

Tabulando quedaría de la siguiente manera:

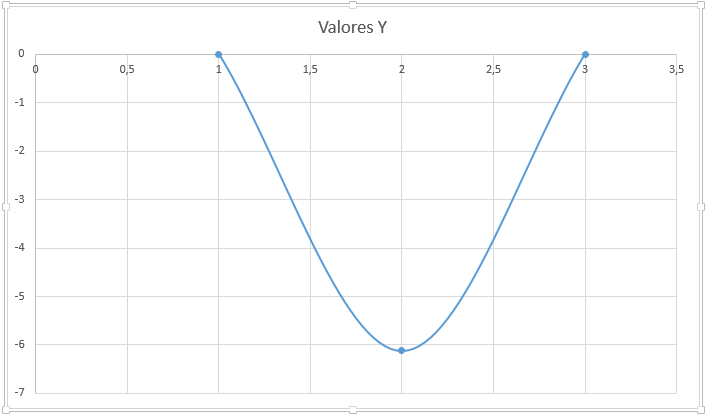
En base a esta información podemos representarlo de forma gráfica, elaborando una parábola, como la siguiente:

Y así, concluimos el problema con la conclusión de que se pueden cercar de 0 a 1800 metros cuadrados del terreno.

Elementos de la Parábola (representación de funciones cuadráticas)

Los elementos o características de una parábola son:

. Orientación o concavidad

. Eje de Simetría

. Vértice 

Orientación o Concavidad:

Se habla de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus brazos o ramas se orientan hacia abajo.

Ésta distinta orientación se define por el valor que tenga el término cuadrático    ax^2. Además, cuanto mayor sea a (el valor absoluto de a), más cerrada es la parábola.

Eje de Simetría:

Es la recta vertical que divide a ésta en dos partes iguales.

Su ecuación está dada por:

X=X1 + X2 

Donde X1 y X2 son las raíces de la ecuación de segundo grado en X, asociada a la parábola. Se puede establecer la ecuación eje de simetría de la parábola:

X= - (B / 2A)

Vértice:

El vértice de la parábola es el punto de corte o intersección del eje de simetría con la parábola y tiene como coordenadas:

(-(b/2a), -(b^2-4ac/4a))

La abscisa de este punto corresponde al valor del eje de simetría (-(b/2a) y la ordenada corresponde al valor máximo o mínimo de la función, (-(b^2-4ac/4a)) según sea la orientación de la parábola.

Fuentes de Internet:

http://www.dav.sceu.frba.utn.edu.ar/homovidens/Marcela%20Martinez/funcion_cuadratica_caracteristicas_nuevo.htm

http://www.aularagon.org/files/espa/ON_Line/matematicas/CMMC5Funciones/CMMC7Complementarias_3.htm