Rectas y Segmentos más Importantes de un Circulo.

Cuerda:

Es un segmento que une dos puntos de la circunferencia sin pasar por su centro. Una cuerda define a un arco, que es un segmento de la circunferencia de menor tamaño que la misma.

Secante:

Es la recta que corta al circulo en dos partes, una más grande que la otra.

Tangente:

Es la recta que toca al circulo en un solo punto; es perpendicular al radio, cuyo extremo es el punto de tangencia.

Radio:

Es un segmento que une al centro con un punto de la circunferencia perimetral.

Diámetro:

Es un segmento que une dos puntos de la circunferencia pasando por el centro. El diámetro divide al círculo en dos partes iguales.

Ejercicio 8 - Construcción de un Pentágono Dentro de una Circunferencia

1.- Traza un diámetro (AB) y después una recta perpendicular (CD (mediatriz).
2.- Traza el radio de uno de los puntos del diámetro (AB), de modo que corte la circunferencia (puntos E,F).
3.- Traza una recta con los puntos de corte (EF), de modo que intersecte el diámetro, el cual será el punto G.
4.- Traza nuevamente el radio del circulo desde punto G, de modo que corte el diámetro, que será el punto H.
5.- Abre el compás del punto C al punto H y realiza cortes a la circunferencia con esa medida, situandote como punto de inicio en el punto C
6.- Une los puntos de corte de la circunferencia que realizaste anteriormente (5).

Ejercicio 7 - Construcción de un Triángulo

1.- Trazar el diámetro y el punto centro (radio).

2.- Trazar el radio por cualquiera de los dos lados del diámetro (segmento AB).

3.- Unir el punto contrario del diámetro (B) con los puntos formados por el radio del arco (C,D).

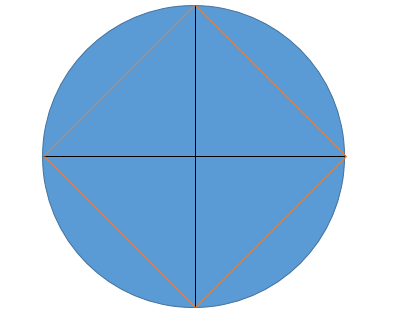
Ejercicio 6 - Polígonos, Construcción de un Cuadrado Dentro de un Circulo.

Los polígonos son figuras formadas por más de 3 lados, los cuales forman su perímetro. Existen polígonos irregulares, los cuales son formados por lados de diferente longitud y los polígonos regulares, que son formados por los lados con la misma longitud.

Construcción de un cuadrado dentro de un circulo cualquiera:

1) Trazamos el diámetro y se traza una perpendicular, haciendo una mediatriz, se intersectan los arcos formados.

2) Los puntos formados en la circunferencia se unen, formando el cuadrado.

Ejercicio 5 - Desigualdad de los Triángulos.

Postulado de la Desigualdad:

En todo triángulo la suma de dos de sus lados cualquiera debe ser mayor a la medida del lado restante.

Determina si se pueden formar los triángulos con las siguientes medidas e indica que clase de triángulo es.

a) 4, 5 y 7
b)6,7 y 13

4+5= 9>7
5+7=12>4          Si se puede.
4+7=11>5

6+7=13=13 x
7+13=20>6        No se puede.
6+13=19>7

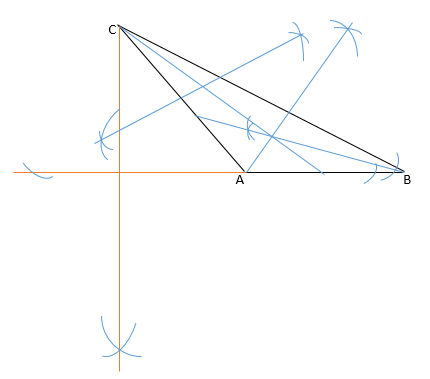
Ejercicio 4 - Ángulos Congruentes.

En el siguiente triángulo:

a) Construye la mediatriz de ___
                                         AC
b) Traza la bisectriz de <B.

c) Traza la mediana de ____
                                  AB 

d) Construye la altura desde el vértice A al lado ___
                                                                    BC 

e) Construye la altura desde el vértice C a la prolongación del lado ____
                                                                                               AB  

Ejercicio 3 - Triángulos

Mediatriz:

Es cada una de las rectas perpendiculares trazadas a un lado por su punto medio (linea trazada a la mitad de un lado). Se obtiene por circuncentro (punto de corte de las 3 mediatrices).

Bisectriz:

Es cada una de las rectas que divide a un ángulo a 2 ángulos iguales. Se obtienen por incentro (punto de corte de las tres bicectrices)

Altura:

Es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o prolongación). Se obtiene ortocentro (punto de corte de las tres alturas).

Mediana:

Es cada una de las rectas que une el punto medio de un lado con el vértice opuesto. Se obtiene el baricentro (punto de corte de las tres medianas).